Este artículo presenta una guía práctica sobre las técnicas de interpolación determinista en el análisis espacial de datos geológicos. Se exploran diversos métodos, desde regresiones de superficies hasta triangulaciones y métodos de inverso de la distancia, ilustrados con ejemplos de modelado de litio en Coipasa. Descubrirás cómo cada técnica aborda la inferencia espacial, sus ventajas y limitaciones, y cómo visualizar los resultados a través de curvas de iso-niveles.
Análisis espacial, datos geológicos, interpolación determinista, regresión de superficies, triangulación de Delaunay, poligonalización de Voronoi, inverso de la distancia, modelado de litio, curvas de iso-niveles, Coipasa.
Contenido:
- Introducción a la Inferencia Espacial en Modelos Determinísticos:
- La inferencia espacial busca estimar valores en ubicaciones no muestreadas a partir de datos existentes.
- Los modelos determinísticos asumen una relación fija entre las variables, representada por una ecuación, y minimizan la suma de los cuadrados de las diferencias entre los valores observados y estimados.
- Regresiones de Superficies:
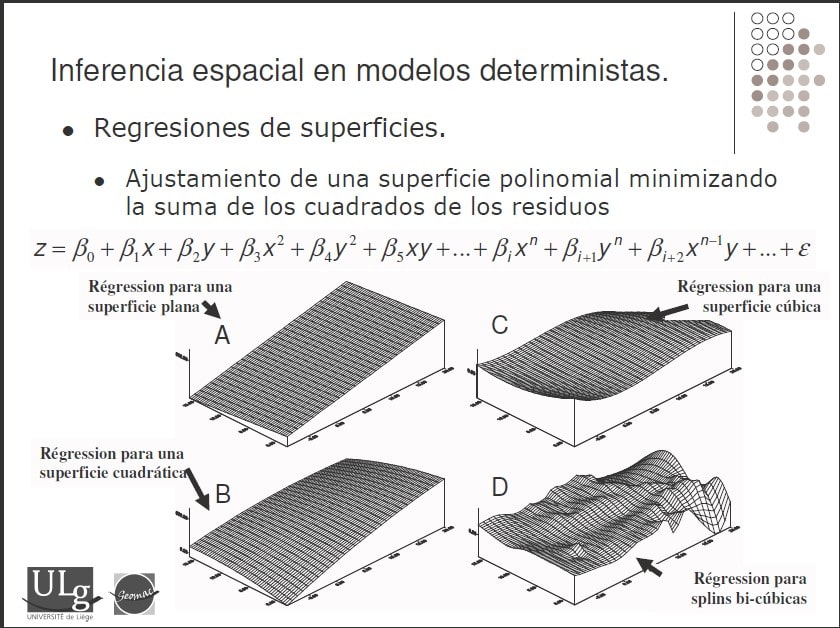
- Ajustan una función matemática a los datos para representar la superficie de la variable de interés.
- Se pueden utilizar diferentes grados de polinomios, desde planos hasta superficies cúbicas, para modelar la complejidad de la superficie.
- Ejemplo: Modelado del litio en Coipasa utilizando regresión cúbica.
- Análisis del Vecino Próximo:
- Asigna el valor del punto de datos más cercano a la ubicación no muestreada.
- Genera una superficie escalonada que refleja la distribución espacial de los datos.
- Ejemplo: Modelado del litio en Coipasa utilizando una malla de 2×2 km.
- Poligonalizaciones y Extensiones:
- Poligonalización de Voronoi: Divide el espacio en polígonos, donde cada polígono contiene un único punto de datos y todos los puntos dentro del polígono están más cerca de ese punto que de cualquier otro.
- Triangulación de Delaunay: Conecta los puntos de datos para formar triángulos, creando una red irregular.
- La extensión de leyes a partir de polígonos puede subestimar las reservas si el valor de corte es mayor que la media.
- Triangulaciones:
- Triangulación Irregular Network (TIN): Representa la superficie como una serie de triángulos interconectados, cada uno definido por tres puntos de datos.
- La ecuación de un plano que pasa por tres puntos permite estimar valores en cualquier punto dentro del triángulo.
- Ejemplo: Modelado del litio en Coipasa utilizando triangulación.
- Inverso de la Distancia:
- Estima valores en ubicaciones no muestreadas ponderando los valores de los puntos de datos cercanos por el inverso de su distancia.
- Inverso de la Distancia al Cuadrado (ISD): Da mayor peso a los puntos más cercanos.
- Ejemplo: Modelado del litio en Coipasa utilizando ISD con un radio de 34 km.
- Visualización en Curvas de Iso-Niveles:
- Las curvas de iso-niveles conectan puntos con el mismo valor, permitiendo visualizar la distribución espacial de la variable.
- Se pueden utilizar diferentes métodos de interpolación para generar las curvas de iso-niveles, lo que resulta en diferentes representaciones de la superficie.
Autor:
Prof. Eric PIRARD (ULg)
Fecha de Publicación:
No se especifica en las fuentes.
Link de descarga: Aquí