¿Te encuentras analizando datos geológicos y no sabes por dónde empezar? ¡Este artículo es tu brújula! Te guiará a través del análisis univariable, una técnica esencial para comprender la distribución de una sola variable. Aprenderás a crear e interpretar histogramas, diagramas de caja y bigotes, y gráficos de frecuencias acumuladas. Descubrirás cómo identificar valores atípicos, calcular medidas de tendencia central y dispersión, y aplicar leyes de densidad probabilística. ¡Domina el análisis univariable y extrae información valiosa de tus datos geológicos!
Análisis Univariable, Datos Geológicos, Histogramas, Diagramas de Caja, Frecuencias Acumuladas, Distribuciones, Valores Atípicos, Coherencia de Datos, Visualización de Datos, Media, Mediana, Moda, Varianza, Desviación Estándar, Ley Normal, Ley Lognormal, Ley de Poisson.
Contenido:
- Visualización de Datos Univariables:
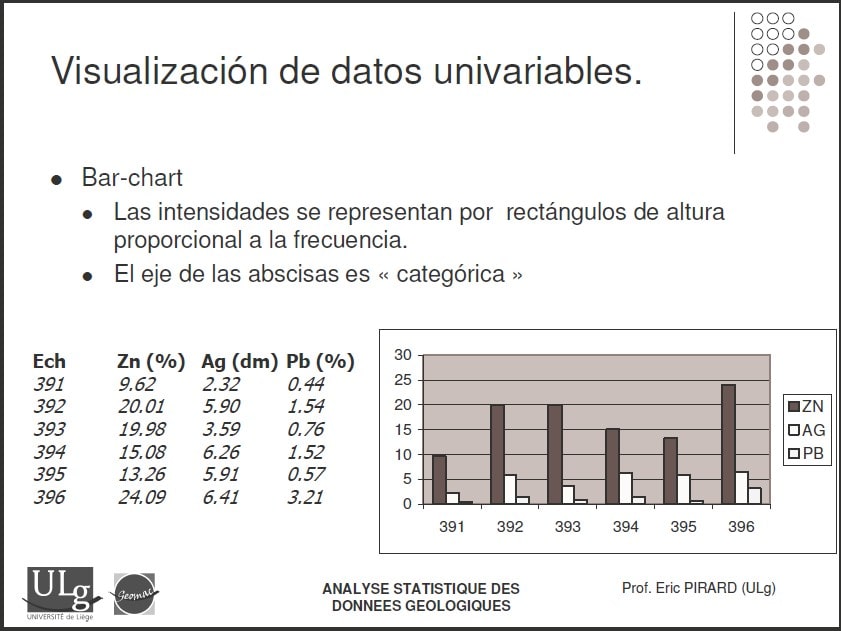
- Gráficos de Barras: Ideales para variables categóricas, representan la frecuencia de cada categoría con la altura de una barra.
- Histogramas: Dividen la escala de la variable en clases y representan la frecuencia de cada clase con la altura de una barra. El número de clases afecta la legibilidad del histograma, se recomienda entre 15 y 20 clases.
- Histogramas de Frecuencias Acumuladas: Muestran el porcentaje acumulado de observaciones hasta un determinado valor de la variable, facilitando la lectura de percentiles.
- Diagramas de Caja y Bigotes: Ofrecen una visión sintética de la distribución de la variable, mostrando los valores mínimo, máximo, mediana (P50) y los percentiles 25 (P25) y 75 (P75).
- Interpretación de Histogramas:
- Simetría y Asimetría: La forma del histograma revela la simetría o asimetría de la distribución de la variable.
- Valores Extremos (Outliers): Identifica valores atípicos que pueden indicar errores de medición o eventos inusuales.
- Multimodalidad: La presencia de varios picos en el histograma sugiere la existencia de diferentes poblaciones dentro de los datos.
- Coherencia en los Datos Univariables:
- Naturaleza, Soporte y Aditividad: Es crucial que las variables analizadas compartan la misma naturaleza (método de análisis, instrumento), el mismo soporte (tamaño de la muestra, escala de medición) y sean aditivas (la suma de las partes representa el todo) para un análisis consistente.
- Cuantificación de una Distribución:
- Parámetros de Tamaño: Describen la posición de la distribución: Mínimo (P0), Máximo (P100), Moda (Mo), Mediana (M = P50), Media Aritmética, Media Geométrica.
- Recomendaciones Prácticas: La mediana es más robusta que la moda y menos afectada por valores extremos que la media.
- Estimadores Robustos: Media Truncada (calculada en una distribución sin valores extremos) y Media Corta (calculada en un intervalo que contiene el 50% de las observaciones).
- Parámetros de Forma: Describen la dispersión de los datos: Extensión (Rango), Desviación Intercuartílica (P75-P25), Desviación Interpercentil (P84-P16), Varianza (s2), Desviación Típica (s), Coeficiente de Variación.
- Parámetros de Tamaño: Describen la posición de la distribución: Mínimo (P0), Máximo (P100), Moda (Mo), Mediana (M = P50), Media Aritmética, Media Geométrica.
- Medidas de Datos Esféricos:
- Azimut y Pendiente: Convenciones para medir datos direccionales.
- Rosa de Direcciones: Representación gráfica de la distribución de datos direccionales, utilizando un radio proporcional a la raíz cuadrada de la frecuencia para una mejor visualización.
- Vector Medio: Representa la dirección promedio de los datos direccionales, calculado con funciones trigonométricas.
- Dispersión Direccional: Mide la variabilidad de las direcciones alrededor del vector medio.
- Leyes de Densidad Probabilística:
- Ley de Poisson: Modela eventos raros e independientes en el tiempo o espacio.
- Ley Normal o Gausiana: Describe eventos con múltiples causas independientes, es simétrica y se caracteriza por su media y desviación estándar.
- Ley Lognormal: Se usa para datos asimétricos donde los logaritmos de los valores siguen una distribución normal.
- Inferencia Estadística:
- Estimación de Parámetros: Permite estimar la media (µ) y la desviación típica (σ) de una población a partir de una muestra.
- Intervalos de Confianza: Establecen un rango de valores que contiene el valor real del parámetro con una cierta probabilidad.
- Pruebas de Hipótesis: Comparan grupos de datos para determinar si provienen de la misma población.
- Clasificación: Asigna observaciones a diferentes poblaciones según su probabilidad de pertenencia.
Autor: Prof. Eric PIRARD (ULg)
Fecha de Publicación: No se proporciona en el documento.
Link de descarga: Aquí